Exercise 2.1
Question 1:
(iii) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.
(iv) The number of zeroes is 2 as the graph intersects the x-axis at 2 points.
(v) The number of zeroes is 4 as the graph intersects the x-axis at 4 points.
(vi) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.
Exercise 2.2
Question 1:
Question 2:
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
Answer :
Exercise 2.3
Question 1:
Question 1:
The graphs
of y = p(x) are given in following figure, for
some polynomials p(x). Find the number of zeroes of
p(x), in each case.
Answer:
(i) The number of zeroes is 0 as the graph does not cut the x-axis at any point.
(ii) The number of zeroes is 1 as the graph intersects the x-axis
at only 1 point.
Answer:
(i) The number of zeroes is 0 as the graph does not cut the x-axis at any point.
(iii) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.
(iv) The number of zeroes is 2 as the graph intersects the x-axis at 2 points.
(v) The number of zeroes is 4 as the graph intersects the x-axis at 4 points.
(vi) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.
Exercise 2.2
Question 1:
Find the
zeroes of the following quadratic polynomials and verify the
relationship between the zeroes and the coefficients.
i) x² – 2x – 8 (ii) 4s² – 4s + 1 (iii) 6x² – 3 – 7x
Answer:
i) x² – 2x – 8 (ii) 4s² – 4s + 1 (iii) 6x² – 3 – 7x
(iv) 4u² + 8u (v) t² – 15 (vi) 3x² – x – 4
Answer:
Question 2:
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
Answer :
Exercise 2.3
Question 1:
Divide the
polynomial p(x) by the polynomial g(x)
and find the quotient and remainder in each of the following:
Answer:
Quotient = x - 3
Remainder = 7x - 9
Quotient = x2 + x - 3
Remainder = 8
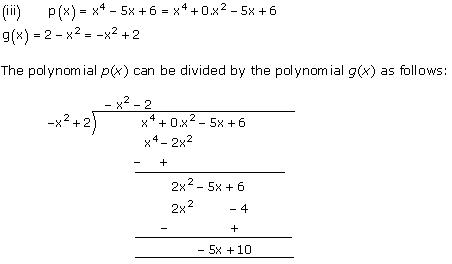
Quotient = -x2 - 2
Remainder = -5x + 10
Concept insight: While dividing one polynomial by another, first arrange the polynomial in descending powers of the variable. In the process of division, be careful about the signs of the coefficients of the terms of the polynomials. After performing division, one can check his/her answer obtained by the division algorithm which is as below:
Dividend = Divisor x Quotient + Remainder
Also, remember that the quotient obtained is a polynomial only.
Question 2:
Answer:
Quotient = x - 3
Remainder = 7x - 9
Quotient = x2 + x - 3
Remainder = 8
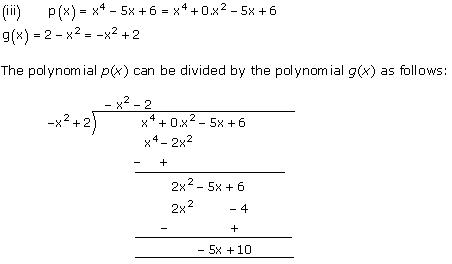
Quotient = -x2 - 2
Remainder = -5x + 10
Concept insight: While dividing one polynomial by another, first arrange the polynomial in descending powers of the variable. In the process of division, be careful about the signs of the coefficients of the terms of the polynomials. After performing division, one can check his/her answer obtained by the division algorithm which is as below:
Dividend = Divisor x Quotient + Remainder
Also, remember that the quotient obtained is a polynomial only.
Question 2:
Check
whether the first polynomial is a factor of the second polynomial by
dividing the second polynomial by the first polynomial:
Answer:
i) The polynomial 2t4 + 3t3 - 2t2 - 9t - 12 can be divided by the polynomial t2 - 3 = t2 + 0.t - 3 as follows:
(
Since the remainder is 0, t² - 3 is a factor of 2t4 + 3t3 - 2t2 - 9t - 12 .
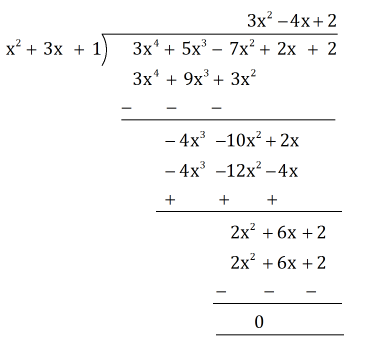
Question 3:
Answer:
Let p(x) = 3x4 + 6x3 - 2x2 - 10x -5
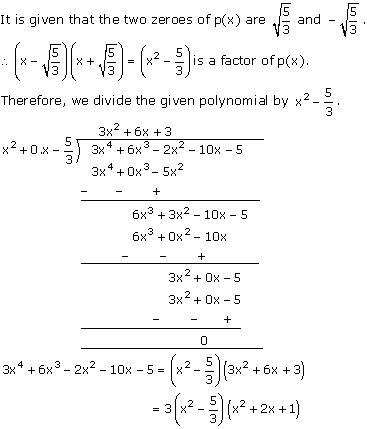
Now, x² + 2x + 1 = (x + 1)2
So, the two zeroes of x² + 2x + 1 are -1 and -1.
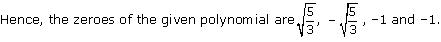
Question 4:
On dividing x³-3x²+x+2 by a polynomial g(x), the quotient and remainder were x – 2
and –2x + 4, respectively. Find g(x).
Answer:
Divided, p(x) = x3 - 3x2 + x + 2
Quotient = (x - 2)
Remainder = (-2x + 4)
Let g(x) be the divisor.
According to the division algorithm,
Dividend = Divisor x Quotient + Remainder
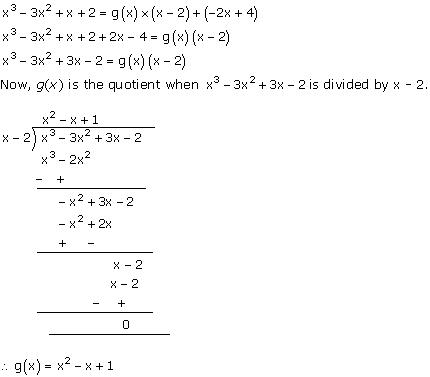
Concept insight: When a polynomial is divided by any other non-zero polynomial, then it satisfies the division algorithm which is as below:
Dividend = Divisor x Quotient + Remainder
Divisor x Quotient = Dividend - Remainder
So, from this relation, the divisor can be obtained by dividing the result of (Dividend - Remainder) by the quotient.
Question 5:
Question 1:
Answer:
i) The polynomial 2t4 + 3t3 - 2t2 - 9t - 12 can be divided by the polynomial t2 - 3 = t2 + 0.t - 3 as follows:
Since the remainder is 0, t² - 3 is a factor of 2t4 + 3t3 - 2t2 - 9t - 12 .
(ii) The polynomial 3x4 + 5x3 - 7x2 + 2x + 2 can be divided by the polynomial x2 + 3x + 1 as follows:
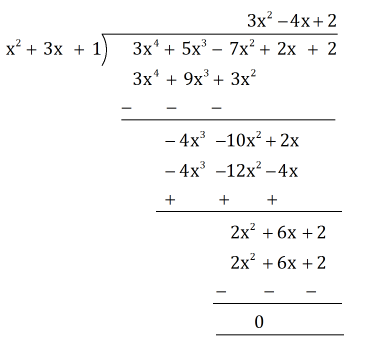
Since the remainder is 0, x² + 3x + 1 is a factor of 3x4 + 5x3 - 7x2 + 2x + 2
(iii) The polynomial x5 - 4x3 + x2 + 3x + 1 can be divided by the polynomial x3 - 3x + 1 as follows:
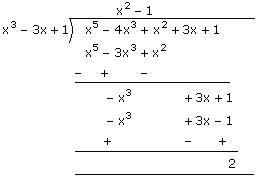
Since the remainder is not equal to 0, x3 - 3x + 1 is not a factor of x5 - 4x3 + x2 + 3x + 1.
(iii) The polynomial x5 - 4x3 + x2 + 3x + 1 can be divided by the polynomial x3 - 3x + 1 as follows:
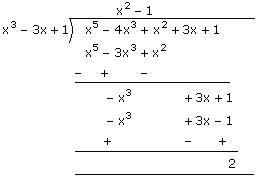
Since the remainder is not equal to 0, x3 - 3x + 1 is not a factor of x5 - 4x3 + x2 + 3x + 1.
Question 3:
Answer:
Let p(x) = 3x4 + 6x3 - 2x2 - 10x -5
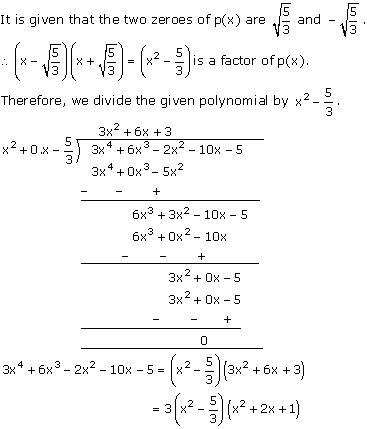
Now, x² + 2x + 1 = (x + 1)2
So, the two zeroes of x² + 2x + 1 are -1 and -1.
Question 4:
On dividing x³-3x²+x+2 by a polynomial g(x), the quotient and remainder were x – 2
and –2x + 4, respectively. Find g(x).
Answer:
Divided, p(x) = x3 - 3x2 + x + 2
Quotient = (x - 2)
Remainder = (-2x + 4)
Let g(x) be the divisor.
According to the division algorithm,
Dividend = Divisor x Quotient + Remainder
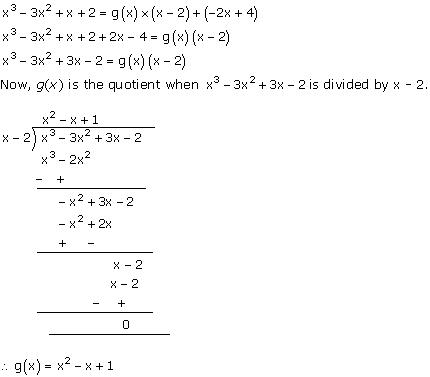
Concept insight: When a polynomial is divided by any other non-zero polynomial, then it satisfies the division algorithm which is as below:
Dividend = Divisor x Quotient + Remainder
Divisor x Quotient = Dividend - Remainder
So, from this relation, the divisor can be obtained by dividing the result of (Dividend - Remainder) by the quotient.
Question 5:
Give
examples of polynomial p(x), g(x), q(x)
and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Answer:
According to the division algorithm, if p(x) and g(x) are two polynomials with g(x)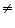
0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x) x q(x) + r(x), where r(x) = 0 or degree of r(x) < degree of g(x).
(i) Degree of quotient will be equal to degree of dividend when divisor is constant.
Let us consider the division of 18x2 + 3x + 9 by 3.
Here, p(x) = 18x2 + 3x + 9 and g(x) = 3
q(x) = 6x2 + x + 3 and r(x) = 0
Here, degree of p(x) and q(x) is the same which is 2.
Checking:
p(x) = g(x) x q(x) + r(x)
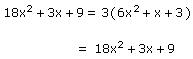
Thus, the division algorithm is satisfied.
(ii) Let us consider the division of 2x4 + 2x by 2x3,
Here, p(x) = 2x4 + 2x and g(x) = 2x3
q(x) = x and r(x) = 2x
Clearly, the degree of q(x) and r(x) is the same which is 1.
Checking,
p(x) = g(x) x q(x) + r(x)
2x4 + 2x = (2x3 ) x x + 2x
2x4 + 2x = 2x4 + 2x
Thus, the division algorithm is satisfied.
(iii) Degree of remainder will be 0 when remainder obtained on division is a constant.
Let us consider the division of 10x3 + 3 by 5x2.
Here, p(x) = 10x3 + 3 and g(x) = 5x2
q(x) = 2x and r(x) = 3
Clearly, the degree of r(x) is 0.
Checking:
p(x) = g(x) x q(x) + r(x)
10x3 + 3 = (5x2 ) x 2x + 3
10x3 + 3 = 10x3 + 3
Thus, the division algorithm is satisfied.
Exercise 2.4(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Answer:
According to the division algorithm, if p(x) and g(x) are two polynomials with g(x)
0, then we can find polynomials q(x) and r(x) such thatp(x) = g(x) x q(x) + r(x), where r(x) = 0 or degree of r(x) < degree of g(x).
(i) Degree of quotient will be equal to degree of dividend when divisor is constant.
Let us consider the division of 18x2 + 3x + 9 by 3.
Here, p(x) = 18x2 + 3x + 9 and g(x) = 3
q(x) = 6x2 + x + 3 and r(x) = 0
Here, degree of p(x) and q(x) is the same which is 2.
Checking:
p(x) = g(x) x q(x) + r(x)
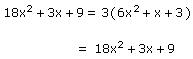
Thus, the division algorithm is satisfied.
(ii) Let us consider the division of 2x4 + 2x by 2x3,
Here, p(x) = 2x4 + 2x and g(x) = 2x3
q(x) = x and r(x) = 2x
Clearly, the degree of q(x) and r(x) is the same which is 1.
Checking,
p(x) = g(x) x q(x) + r(x)
2x4 + 2x = (2x3 ) x x + 2x
2x4 + 2x = 2x4 + 2x
Thus, the division algorithm is satisfied.
(iii) Degree of remainder will be 0 when remainder obtained on division is a constant.
Let us consider the division of 10x3 + 3 by 5x2.
Here, p(x) = 10x3 + 3 and g(x) = 5x2
q(x) = 2x and r(x) = 3
Clearly, the degree of r(x) is 0.
Checking:
p(x) = g(x) x q(x) + r(x)
10x3 + 3 = (5x2 ) x 2x + 3
10x3 + 3 = 10x3 + 3
Thus, the division algorithm is satisfied.
Question 1:
Verify
that the numbers given alongside of the cubic polynomials below are
their zeroes. Also verify the relationship between the zeroes and the
coefficients in each case:
Answer:
On comparing the given polynomial with the polynomial ax3 + bx2 + cx + d, we obtain a = 2, b = 1, c = -5, d = 2
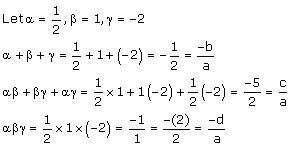
Thus, the relationship between the zeroes and the coefficients is verified.
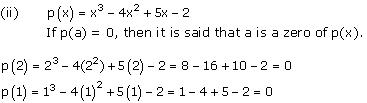
On comparing the given polynomial with the polynomial ax3 + bx2 + cx + d, we obtain a = 1, b = -4, c = 5, d = -2.
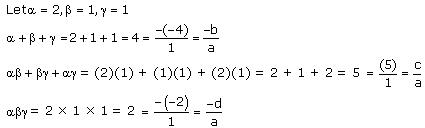
Thus, the relationship between the zeroes and the coefficients is verified.
Question 2:
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, − 7, − 14 respectively.
Answer:
Let the polynomial be ax3 + bx2 + cx + d and its zeroes be
.
According to the given information:
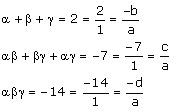
If a = k, then b = -2k, c = -7k, d = 14k
Thus, the required cubic polynomial is k(x3 - 2x2 - 7x + 14), where k is any real number.
The simplest polynomial will be obtained by taking k = 1.
Question 3:
If the zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a, a + b, find a and b.
Answer:
Let p(x) = x3 - 3x2 + x + 1
The zeroes of the polynomial p(x) are given as a - b, a, a + b.
Comparing the given polynomial with dx3 + ex2 + fx + g, we can observe that
d = 1, e = -3, f = 1, g = 1
Therefore, the zeroes of p(x) are 1-b, 1, 1+b .
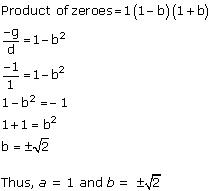
Question 4:
Answer:
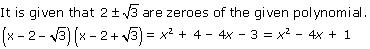
Therefore, x2 - 4x + 1 is a factor of the given polynomial.
Question 5:
Answer:
On comparing the given polynomial with the polynomial ax3 + bx2 + cx + d, we obtain a = 2, b = 1, c = -5, d = 2
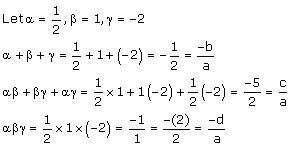
Thus, the relationship between the zeroes and the coefficients is verified.
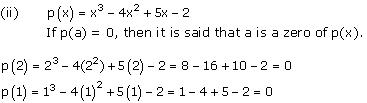
On comparing the given polynomial with the polynomial ax3 + bx2 + cx + d, we obtain a = 1, b = -4, c = 5, d = -2.
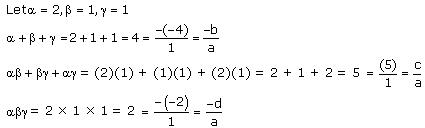
Thus, the relationship between the zeroes and the coefficients is verified.
Question 2:
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, − 7, − 14 respectively.
Answer:
Let the polynomial be ax3 + bx2 + cx + d and its zeroes be
.According to the given information:
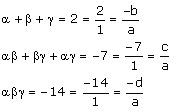
If a = k, then b = -2k, c = -7k, d = 14k
Thus, the required cubic polynomial is k(x3 - 2x2 - 7x + 14), where k is any real number.
The simplest polynomial will be obtained by taking k = 1.
Question 3:
If the zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a, a + b, find a and b.
Answer:
Let p(x) = x3 - 3x2 + x + 1
The zeroes of the polynomial p(x) are given as a - b, a, a + b.
Comparing the given polynomial with dx3 + ex2 + fx + g, we can observe that
d = 1, e = -3, f = 1, g = 1
Therefore, the zeroes of p(x) are 1-b, 1, 1+b .
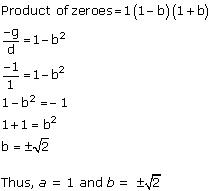
Question 4:
Answer:
Therefore, x2 - 4x + 1 is a factor of the given polynomial.
For finding the remaining zeroes of the given polynomial, we will carry out the division of
Hence, 7 and -5 are also zeroes of the given polynomial.
Hence, 7 and -5 are also zeroes of the given polynomial.
Question 5:
Answer:
By division algorithm,
Dividend = Divisor x Quotient + Remainder
Divisor x Quotient = Dividend - Remainder
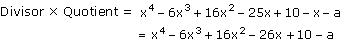
It will be perfectly divisible by x2 - 2x + k.
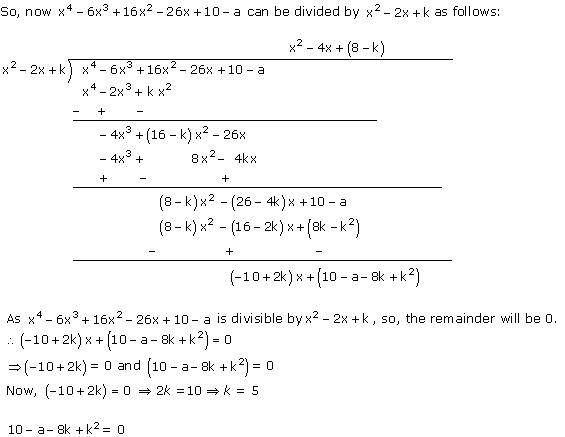
10 - a - 8 x 5 + 25 = 0
10 - a - 40 + 25 = 0
- 5 - a = 0
a = -5
Thus, k = 5 and a = -5.
Dividend = Divisor x Quotient + Remainder
Divisor x Quotient = Dividend - Remainder
It will be perfectly divisible by x2 - 2x + k.
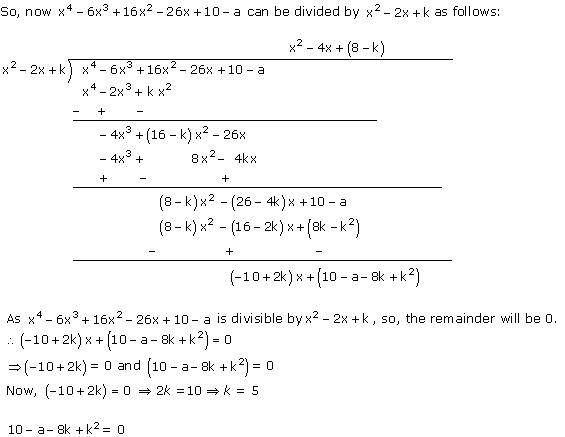
10 - a - 8 x 5 + 25 = 0
10 - a - 40 + 25 = 0
- 5 - a = 0
a = -5
Thus, k = 5 and a = -5.
No comments:
Post a Comment